Simetría especular
.jpg)
_KL.jpg)
En geometría, la simetría especular (también conocida como simetría bilateral o de reflexión), es una transformación con respecto a un plano de simetría, en la que a cada punto de una figura se le asocia otro punto llamado imagen, que cumple las siguientes condiciones:
a) La distancia de un punto y su imagen al plano de simetría, es la misma.
b) El segmento que une un punto con su imagen, es perpendicular al plano de simetría.
Una figura que permanece invariante al someterse a una reflexión se dice que posee simetría especular o de reflexión. En el caso de figuras en un plano bidimensional, el plano de simetría se convierte en un eje de simetría.
Teoría de cuerdas
[editar]La simetría especular es una relación que puede existir entre dos variedades de Calabi-Yau. Generalmente se puede dar entre dos de tales variedades hexadimensionales, cuyas formas pueden parecer muy diferentes geométricamente, pero que, sin embargo, son equivalentes si se emplean como dimensiones ocultas de la teoría de cuerdas. Más específicamente, la simetría especular relaciona dos variedades M y W cuyos números de Hodge
- h1,1 y h1,2
se intercambian. Se puede demostrar que la teoría de cuerdas compactada en estas dos variedades conduce a fenómenos físicos idénticos.
El descubrimiento de la simetría especular está ligado con nombres tales como Brian Greene, Ronen Plesser, Philip Candelas, Monika Lynker, Rolf Schimmrigk y otros. Andrew Strominger, Shing-Tung Yau, y Eric Zaslow han demostrado que la simetría especular es un ejemplo especial de la dualidad T: la variedad de Calabi-Yau se puede describir como un fibrado cuya fibra sea un toro tridimensional. La acción simultánea de la dualidad T en las tres dimensiones de este toro es equivalente a la simetría especular.
La simetría especular permite simplificar muchos cálculos, invocando la imagen especular de una situación física dada, que puede ser a menudo mucho más fácil de resolver.
Geometría analítica
[editar]- El punto (x,y,z) y (-x,y,z) son simétricos respecto al plano Oyz
- El punto (x,y,z) y (x,-y,z) son simétricos respecto al plano Oxz
- El punto (x,y,z) y (x,y, -z) son simétricos respecto al plano Oxy
Geometría del espacio
[editar]- El cubo es una figura simétrica respecto al plano que pasa por las rectas que contienen a las diagonales de dos caras opuestas.
- El cubo es una figura simétrica respecto al plano que pasa por los puntos medios de las cuatro aristas perpendiculares a dos caras opuestas.
- El plano que contiene a dos diagonales del cubo es una plano de simetría del cubo.
Ejemplos
[editar]
En dos dimensiones, la simetría se verifica respecto a una línea recta o eje de simetría, y en tres dimensiones respecto a un plano de simetría. Un objeto o figura que es indistinguible de su imagen transformada se denomina imagen especular. Resumidamente, una línea de simetría divide la forma en dos mitades exactas abatibles entre sí.
Funciones simétricas
[editar]
En términos formales, un objeto matemático es simétrico con respecto a una operación definida como reflexión, rotación o traslación, si, cuando se aplica al objeto, esta operación conserva alguna propiedad del objeto.[1] El conjunto de operaciones que preservan una propiedad dada del objeto forman un grupo. Dos objetos son simétricos entre sí con respecto a un grupo de operaciones dado si uno se obtiene del otro mediante algunas de las operaciones (y viceversa).
Se dice que la gráfica bidimensional de una función es simétrica si existe al menos una línea recta o eje tal que todas sus perpendiculares que intersecan la gráfica a una cierta distancia del eje, también la intersecan en sentido opuesto a la misma distancia.
Otra forma de pensar en una función simétrica es que si la forma se doblara por la mitad respecto al eje, las dos mitades serían idénticas: las dos mitades son imagen especular una de la otra.[1]
Por lo tanto, un cuadrado tiene cuatro ejes de simetría, porque existen cuatro formas diferentes de doblarlo y hacer que todos los bordes coincidan. Un círculo tiene infinitos ejes de simetría.
Formas geométricas simétricas
[editar]
|
|
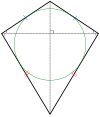
| Trapecio isósceles y deltoide | |
|---|---|
|
|
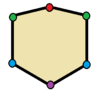
| Hexágonos | |
|
|
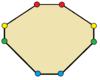
| Octógonos | |
Los Triángulo con simetría de reflexión son triángulo isósceles. Los cuadriláteros con simetría de reflexión son deltoides, deltoides (cóncavos), rombos,[2] y trapecios isósceles. Todos los polígonos regulares de lados pares tienen dos formas de reflexión simples, una con ejes de reflexión a través de vértices opuestos y otra con ejes a través del centro de lados opuestos.
Para una forma arbitraria, la axialidad de la forma mide su proximidad a ser simétrica bilateralmente. Es igual a 1 para formas con simetría de reflexión y entre 2/3 y 1 para cualquier forma convexa.
Equivalentes matemáticos
[editar]Para cada eje o plano de reflexión, el grupo de simetría es isomorfo con Cs (véase grupos de puntos en tres dimensiones), uno de los tres tipos de orden dos (involuciones), por lo tanto algebraicamente C2. El dominio fundamental es un semiplano o semiespacio.
En ciertos contextos, existe una simetría de rotación y de reflexión. Entonces, la simetría de la imagen especular es equivalente a la simetría de inversión; en tales contextos en la física moderna, el término paridad o P-simetría se usa para ambos.
Tipos avanzados de simetría de reflexión
[editar]Para tipos más generales de reflexión, en consecuencia existen tipos más generales de simetría de reflexión. Por ejemplo:
- Con respecto a una involución afín no isométrica (una simetría oblicua respecto a una línea, plano, etc.)
- Con respecto a una inversión circular.
En la naturaleza
[editar]_-_Museo_Civico_di_Storia_Naturale_Giacomo_Doria_-_Genoa,_Italy_-_DSC03222_Cropped.JPG)
Los animales simétricamente bilaterales poseen simetría de reflexión en el plano sagital, que divide el cuerpo verticalmente en mitades izquierda y derecha, con uno de cada par de órganos sensoriales y extremidades a cada lado. La mayoría de los animales son bilateralmente simétricos, probablemente porque esto apoya el movimiento hacia adelante y simplifica su estructura.[3][4][5][6]
En arquitectura
[editar]
La simetría especular se usa a menudo en arquitectura, como en la fachada de la Basílica de Santa María Novella, Florencia.[7] También se encuentra en el diseño de estructuras antiguas como Stonehenge.[8] La simetría fue un elemento central en algunos estilos de arquitectura, como el palladianismo.[9]
Véase también
[editar]Referencias
[editar]- ↑ a b Stewart, Ian (2001). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson. p. 32.
- ↑ Gullberg, Jan (1997). Mathematics: From the Birth of Numbers. W. W. Norton. pp. 394–395. ISBN 0-393-04002-X. (requiere registro).
- ↑ Valentine, James W. «Bilateria». AccessScience. Consultado el 29 de mayo de 2013.
- ↑ «Bilateral symmetry». Natural History Museum. Consultado el 14 de junio de 2014.
- ↑ Finnerty, John R. (2005). «Did internal transport, rather than directed locomotion, favor the evolution of bilateral symmetry in animals?». BioEssays 27 (11): 1174-1180. PMID 16237677. doi:10.1002/bies.20299. Archivado desde el original el 2 de julio de 2019. Consultado el 3 de mayo de 2021.
- ↑ «Bilateral (left/right) symmetry». Berkeley. Consultado el 14 de junio de 2014.
- ↑ Tavernor, Robert (1998). On Alberti and the Art of Building. Yale University Press. pp. 102-106. ISBN 978-0-300-07615-8. «More accurate surveys indicate that the facade lacks a precise symmetry, but there can be little doubt that Alberti intended the composition of number and geometry to be regarded as perfect. The facade fits within a square of 60 Florentine braccia».
- ↑ Johnson, Anthony (2008). Solving Stonehenge: The New Key to an Ancient Enigma. Thames & Hudson.
- ↑ Waters, Suzanne. «Palladianism». Royal Institution of British Architects. Archivado desde el original el 4 de marzo de 2016. Consultado el 29 de octubre de 2015.
Bibliografía
[editar]- Stewart, Ian (2001). What Shape is a Snowflake? Magical Numbers in Nature. Weidenfeld & Nicolson.
- Weyl, Hermann (1982 (1ª ed. 1952)). Symmetry. Princeton: Princeton University Press. ISBN 0-691-02374-3.
Enlaces externos
[editar]
Wikimedia Commons alberga una categoría multimedia sobre Simetría especular.- Aplicación con simetría - fuente en Delphi
- Ejemplos de simetría de reflexión de Math Is Fun
| Control de autoridades |
|
|---|
Datos: Q15955882- Multimedia: Reflection symmetry / Q15955882